MECÂNICA GRACELI GENERALIZADA - QUÂNTICA DIMENSIONAL TENSORIAL RELATIVISTA DE CA MPOS 1.270]

MECÂNICA GRACELI GENERALIZADA - QUÂNTICA TENSORIAL DIMENSIONAL RELATIVISTA DE CAMPOS.

MECÃNICA GRACELI GERAL - QTDRC.

$equação Graceli dimensional relativista tensorial quântica de campos$

$\psi ^{*}$

$[$ $\psi ^{*}$ $G$ * $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $T_{\mu \nu }$ $/$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $T_{\mu \nu }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ +

$+$ $G$ * $\psi ^{*}$ [ $\psi ^{*}$ ${\boldsymbol {\mu }}$ ] $\lambda$ ω ${\mathcal {T}}$ , $\sigma$ , $\psi$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ [x,t] ] =

//////

[

$\psi ^{*}$

$TeoriaInteraçãomediadorMagnitude relativaComportamentoFaixaCromodinâmicaForça nuclear forteGlúon10411/r71,4 × 10-15 mEletrodinâmicaForça eletromagnéticaFóton10391/r2infinitoFlavordinâmicaForça nuclear fracaBósons W e Z10291/r5 até 1/r710-18 mGeometrodinâmicaForça gravitacionalgráviton101/r2infinito$

Teoria	Interação	mediador	Magnitude relativa	Comportamento	Faixa
Cromodinâmica	Força nuclear forte	Glúon	1041	1/r7	1,4 × 10-15 m
Eletrodinâmica	Força eletromagnética	Fóton	1039	1/r2	infinito
Flavordinâmica	Força nuclear fraca	Bósons W e Z	1029	1/r5 até 1/r7	10-18 m
Geometrodinâmica	Força gravitacional	gráviton	10	1/r2	infinito

$G* = OPERADOR DE DIMENSÕES DE GRACELI.$

DIMENSÕES DE GRACELI SÃO TODA FORMA DE TENSORES, ESTRUTURAS, ENERGIAS, ACOPLAMENTOS, , INTERAÇÕES DE CAMPOS E ENERGIAS, DISTRIBUIÇÕES ELETRÔNICAS, ESTADOS FÍSICOS, ESTADOS QUÂNTICOS, ESTADOS FÍSICOS DE ENERGIAS DE GRACELI, E OUTROS.

/ $G$ * $\psi ^{*}$ [ $\psi ^{*}$ $T_{\mu \nu }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$

MECÂNICA GRACELI GENERALIZADA - QUÂNTICA TENSORIAL DIMENSIONAL RELATIVISTA DE INTERAÇÕES DE CAMPOS. EM ;

MECÂNICA GRACELI REPRESENTADA POR TRANSFORMADA.

dd = dd [G] = DERIVADA DE DIMENSÕES DE GRACELI.

- [ $G*$ $\hbar$ $.$ $\psi$

G { f [dd]} ´[d] $\psi ^{*}$ $\hbar$ $\psi$ $f [d] G*$ $T_{\mu \nu }$ $\psi$ $dd [G]$

O ESTADO QUÂNTICO DE GRACELI

- [ $G*$ $\hbar$ $.$ $\psi$ $\left|\psi \right\rangle ={\frac {1}{\sqrt {2}}}{\bigg (}\left|\uparrow \downarrow \right\rangle -\left|\downarrow \uparrow \right\rangle {\bigg )},$ ]

$G* = DIMENSÕES DE GRACELI TAMBÉM ESTÁ RELACIONADO COM INTERAÇÕES DE ENERGIAS, QUÂNTICAS, RELATIVÍSTICAS, , E INTERAÇÕES DE CAMPOS.$

o tensor energia-momento $T_{\mu \nu }$ é aquele de um campo eletromagnético,

/ $G$ * $\psi ^{*}$ [ $\psi ^{*}$ $T_{\mu \nu }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$

$G$

A energia de Casimir (e sua força) pode ser calculada a partir da energia do ponto zero do modo de Fourier do campo eletromagnético entre as placas.

A força de Casimir por unidade de área $F_{c}/A$ para placas ideais, perfeitamente condutoras com vácuo entre si é

{F_{c} \over A}={\hbar c\pi ^{2} \over 240d^{4}}

$G$

onde

\hbar

(hbar, ℏ) é a constante reduzida de Planck (às vezes conhecida como constante de Dirac),

�

é a velocidade da luz no vácuo,

�

é a distância entre as duas placas.

Isso mostra que a força Casimir por unidade de área $F_{c}/A$ é muito pequena visto ${\hbar c\pi ^{2} \over 240}\approx 1,3\times 10^{-27}Nm^{2}$ . $G$

O cálculo mostra que a força é proporcional à soma $1+2+3+4+5+\dots$ onde os números $1,2,3,4,5,\dots$ representam as frequências de ondas estacionárias entre as placas; cada possível onda se comporta com um oscilador harmônico quântico cuja energia do estado fundamental é igual a $\hbar \omega /2$ contribui para a energia potencial total; a força então é igual menos o derivativo da energia potencial com respeito a distância.

A série (soma de inteiros) é divergente e precisa ser renormalizada. Uma ferramenta útil é dada pela função zeta de Riemann porque a soma pode ser formalmente escrita como $\zeta (-1)$ que é igual a $-1/12$ . Embora alguns possam acreditar que esse seria um resultado correto para a soma da série $1+2+3+4+5+\dots$ , isso é totalmente incorreto e, se existir algum método rigoroso para se chegar a este resultado, então cabe a esta pessoa o ônus da prova.

A fórmula de Landau–Zener é uma expressão matemática para a probabilidade de transição entre dois níveis de energia numa situação de cruzamento evitado. Corresponde a uma solução analítica das equações de movimento que regem a dinâmica de um sistema mecânico quântico de 2-níveis de energia, com um hamiltoniano dependente do tempo variando de tal forma que a separação de energia dos dois estados (diabáticos) é uma função linear do tempo, e o acoplamento entre esses dois estados é constante. A fórmula foi publicada separadamente por Lev Landau,^[1] Clarence Zener,^[2] Ernst Stueckelberg,^[3] and Ettore Majorana,^[4] em 1932.

Fórmula de Landau-Zener

A fórmula de Landau-Zener tem tido um papel central na descrição de efeitos não-adiabáticos (envolvendo mais do que um estado electrónico) em colisões atómicas e moleculares ^[5] em particular, e efeitos não-adiabáticos na química e física molecular em geral.^[6] Neste contexto, considera-se que o sistema se move com uma velocidade constante v e que a variação ao longo da coordenada z dos níveis de energia do sistema é uma hipérbole. A probabilidade de um sistema que começa num dos níveis de energia terminar no outro nível de energia depois de atravessar o centro da hipérbole em z_c, em que o intervalo que separa os dois níveis de energia é menor, é dada pela fórmula de Landau-Zener

$p_{LZ}=exp\left(-{\frac {\pi ^{2}\Delta V^{2}}{h\Delta Fv}}\right)$ , $G$

em que ΔV é a diferença energética dos dois níveis no ponto z_c, ΔF é a diferença do declive das assimptotas da hipérbole e h é a constante de Planck.

A fórmula de Landau-Zener fornece resultados razoáveis quando a energia cinética do sistema é elevada, mas sobretudo é um modelo paradigmático para racionalizar efeitos não-adiabáticos.^[7]

Fórmula de Stueckelberg

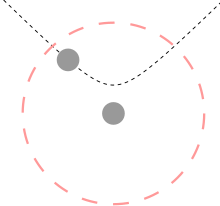
Numa colisão atómica ou molecular, o sistema atravessa por duas vezes a região z_c em que a energia dos dois níveis se aproxima. A probabilidade de um sistema que se encontra num determinado nível de energia antes da colisão e terminar num outro após a colisão, foi determinada por Stueckelberg ^[3]

$p_{S}=4p_{LZ}(1-p_{LZ})\sin ^{2}(\Phi +\varphi )$ , $G$

em que p_LZ é a probabilidade de transição numa passagem dada pela fórmula da Landau-Zener, Φ é a diferença de fases acumulada pela função de onda do sistema entre as duas passagens por z_c, e φ é uma fase dinâmica que tende para φ=π/4 no limite de velocidades elevadas.^[7]

Search This Blog

MECÂNICA GRACELI GENERALIZADA - QUÂNTICA DIMENSIONAL TENSORIAL RELATIVISTA DE CA MPOS 1.270]

Fórmula de Landau-Zener

Fórmula de Stueckelberg

Comments

Post a Comment

Popular posts from this blog